STATISTICAL DISPERSION RELATION FOR SPATIALLY BROADBAND FIELDS

MINGGUANG SHAN, 1,2 VIOREL NASTASA, 1,3 AND GABRIEL POPESCU1,*
Optics Letters, Vol. 41, No. 11 2016

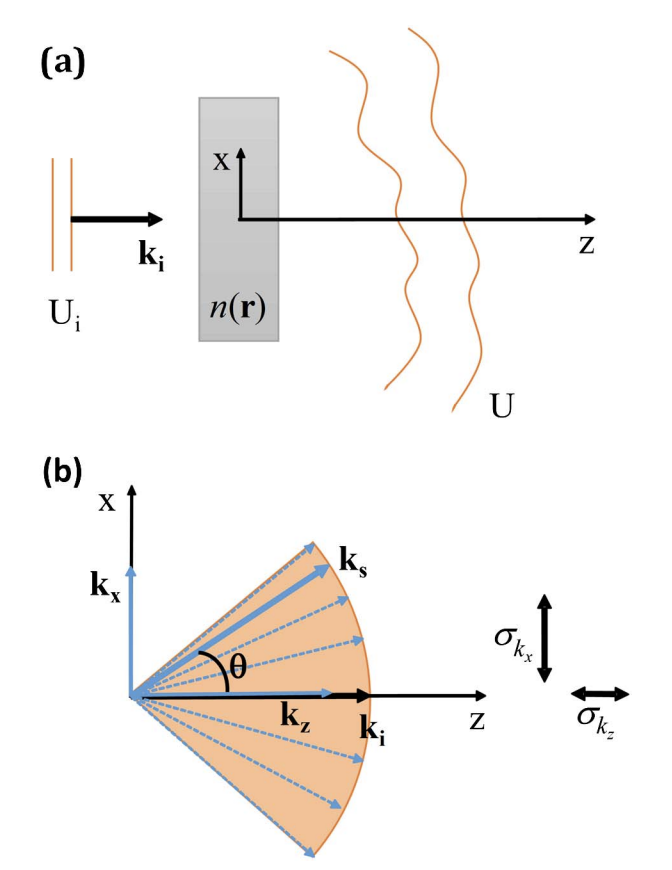
The dispersion relation is fundamental to a physical phenomenon that develops in both space and time. This equation connects the spatial and temporal frequencies involved in the dynamic process through the material constants. Electromagnetic plane waves propagating in homogeneous media are bound by simple dispersion relation, which sets the magnitude of the spatial frequency, , as being proportional to the temporal frequency, , with the proportionality constant dependent on the refractive index, , and the speed of light in vacuum, . Here we show that, for spatially broadband fields, an analog dispersion relation can be derived, except in this case the -vector variance is connected with the temporal frequency through the statistics of the refractive index fluctuations in the medium. We discuss how this relationship can be used to retrieve information about refractive index distributions in biological tissues. This result is particularly significant in measurements of angular light scattering and quantitative phase imaging of biological structures.