DETERMINISTIC SIGNAL ASSOCIATED WITH A RANDOM FIELD, OPT.EXP., 21(18), 20806-20820 (2013)

T. KIM, R. ZHU, T. NGUYEN, R. ZHOU, C. EDWARDS, L. GODDARD AND G. POPESCU
2013

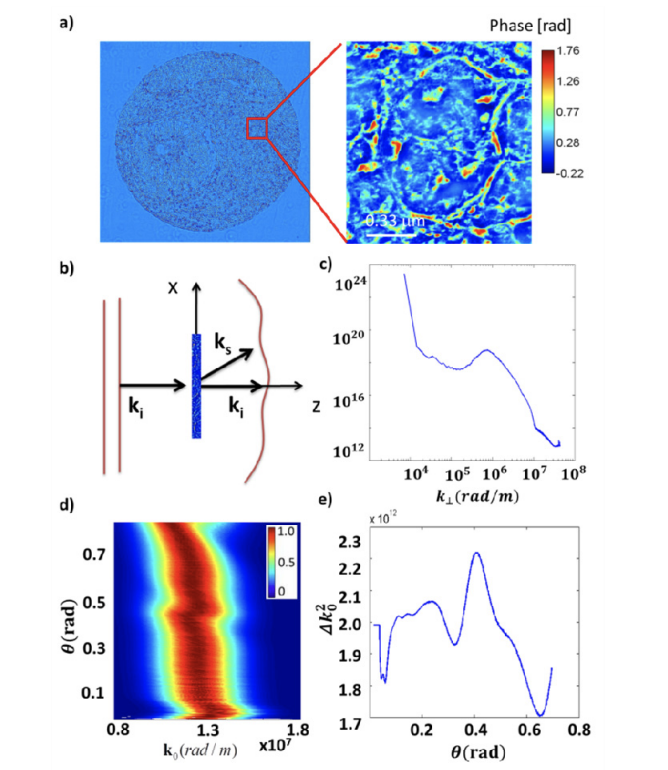
Stochastic fields do not generally possess a Fourier transform. This makes the second-order statistics calculation very difficult, as it requires solving a fourth-order stochastic wave equation. This problem was alleviated by Wolf who introduced the coherent mode decomposition and, as a result, space-frequency statistics propagation of wide-sense stationary fields. In this paper we show that if, in addition to wide-sense stationarity, the fields are also wide-sense statistically homogeneous, then monochromatic plane waves can be used as an eigenfunction basis for the cross spectral density. Furthermore, the eigenvalue associated with a plane wave, exp[i(k⋅r−ωt)], is given by the spatiotemporal power spectrum evaluated at the frequency (k, ω). We show that the second-order statistics of these fields is fully described by the spatiotemporal power spectrum, a real, positive function. Thus, the second-order statistics can be efficiently propagated in the wavevector-frequency representation using a new framework of deterministic signals associated with random fields. Analogous to the complex analytic signal representation of a field, the deterministic signal is a mathematical construct meant to simplify calculations. Specifically, the deterministic signal associated with a random field is defined such that it has the identical autocorrelation as the actual random field. Calculations for propagating spatial and temporal correlations are simplified greatly because one only needs to solve a deterministic wave equation of second order. We illustrate the power of the wavevector-frequency representation with calculations of spatial coherence in the far zone of an incoherent source, as well as coherence effects induced by biological tissues.