WOLF PHASE TOMOGRAPHY (WPT) OF TRANSPARENT STRUCTURES USING PARTIALLY COHERENT ILLUMINATION

Xi Chen 1 , Mikhail E. Kandel 1 , Chenfei Hu 1 , Young Jae Lee1 and Gabriel Popescu 1
Light: Science & Applications 9:142 (2020) 2020

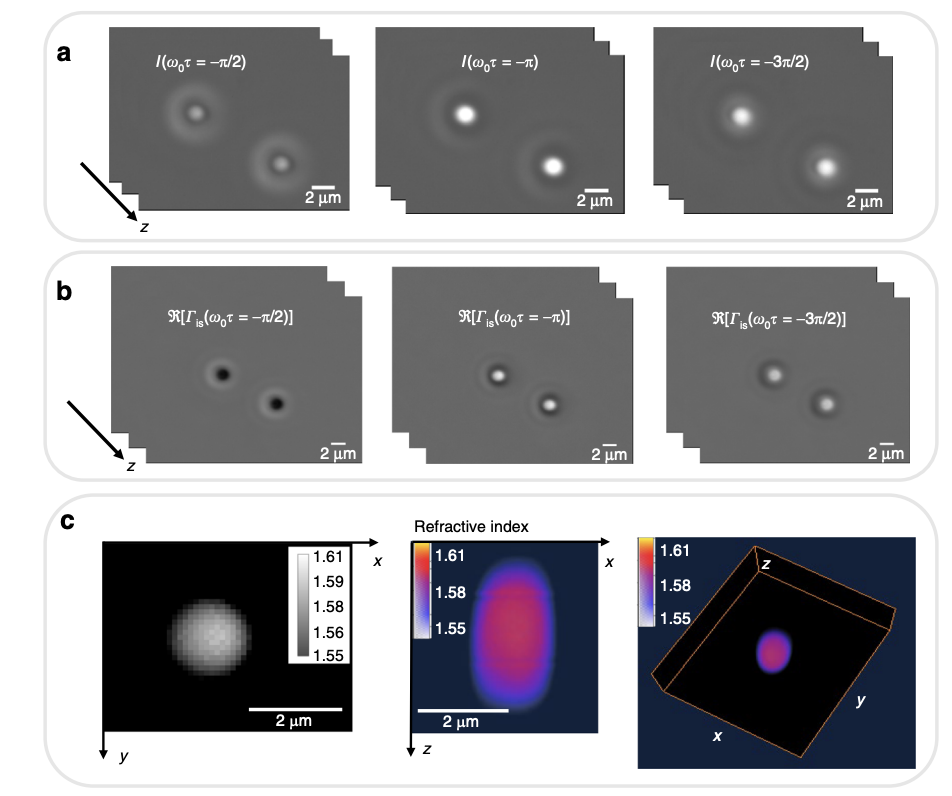
In 1969, Emil Wolf proposed diffraction tomography using coherent holographic imaging to extract 3D information from transparent, inhomogeneous objects. In the same era, the Wolf equations were first used to describe the propagation correlations associated with partially coherent fields. Combining these two concepts, we present Wolf phase tomography (WPT), which is a method for performing diffraction tomography using partially coherent fields. WPT reconstruction works directly in the space–time domain, without the need for Fourier transformation, and decouples the refractive index (RI) distribution from the thickness of the sample. We demonstrate the WPT principle using the data acquired by a quantitative-phase-imaging method that upgrades an existing phase-contrast microscope by introducing controlled phase shifts between the incident and scattered fields. The illumination field in WPT is partially spatially coherent (emerging from a ring-shaped pupil function) and of low temporal coherence (white light), and as such, it is well suited for the Wolf equations. From three intensity measurements corresponding to different phase-contrast frames, the 3D RI distribution is obtained immediately by computing the Laplacian and second time derivative of the measured complex correlation function. We validate WPT with measurements of standard samples (microbeads), spermatozoa, and live neural cultures. The high throughput and simplicity of this method enables the study of 3D, dynamic events in living cells across the entire multiwell plate, with an RI sensitivity on the order of 10^−5.