Diffraction As Scattering Under the Born Approximation

N. Goswami and G. Popescu
Optics Express, Vol. 29, No. 24 / 22 Nov 2021

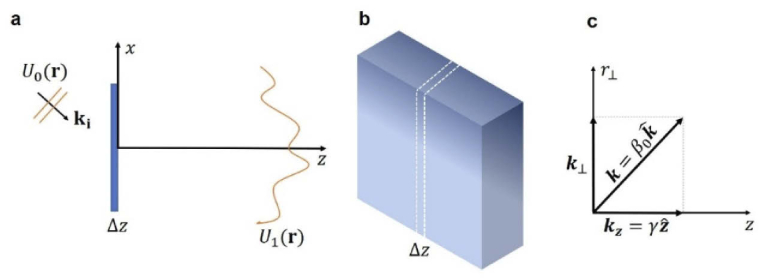
Light diffraction at an aperture is a basic problem that has generated a tremendous amount of interest in optics. Some of the most significant diffraction results are the Fresnel Kirchhoff and Rayleigh-Sommerfeld formulas. These theories are based on solving the wave equation using Green’s theorem and result in slightly different expressions depending on the particular boundary conditions employed. In this paper, we show that the diffraction by a thin screen, which includes apertures, gratings, transparencies etc., can be treated more generally as a particular case of scattering. Furthermore, applying the first order Born approximation to 2D objects, we obtain a general diffraction formula, without angular approximations. Finally, our result, which contains no obliquity factor, is consistent with the 3D theory of scattering. We discuss several common approximations and place our results in the context of existing theories.